A continuación se presenta un vídeo donde se gráfica una función en el programa geogebra, de tal manera que puedes recurrir a programas informáticos para obtener la gráfica de cualquier función real.
las funciones reales se pueden clasificar de acuerdo a su estructura en tres grupos:
FUNCIONES POLINOMICAS
FUNCIÓN LINEAL
Es una función de la forma f(x) = mx + b, donde m es la pendiente y b es la abscisa donde la recta intercepta al eje. La grafica que se origina es una línea recta, si m es positiva la recta se inclina hacia la derecha y si m es negativa la recta se inclina hacia la izquierda.
EJEMPLO:
FUNCIÓN CONSTANTE
Es una función de la forma f(x) = k, donde k es una constante. La grafica que se origina es una línea recta paralela al eje x.
El dominio de la función constante son todos los números reales y el rango es un conjunto unitario formado por el elemento imagen de todos los elementos del dominio.
EJEMPLO:
EJEMPLO:
Ø FUNCIÓN
Es una función de la forma f(x) = ax2+ bx +c, donde a,b,c y son números reales. La grafica de la función cuadrática es una curva llamada parábola; si a es positiva, la grafica abre hacia arriba y si a es negativa la grafica abre hacia abajo.
La ecuación algebraica tiene el 2 como máximo exponente de la variable.
EJEMPLO:
FUNCIÓN POLINOMICA
Una función Polinómica es de la forma f(x) = anxn+an-1xn-1+…+a donde an,an-1,…,a son constantes reales y n es numero entero no negativo que indica el grado de p(x), siempre que an≠0.
Ejemplo:
Ø
FUNCIONES ESPECIALES
FUNCIÓN VALOR ABSOLUTO
FUNCIONES ESPECIALES
FUNCIÓN VALOR ABSOLUTO
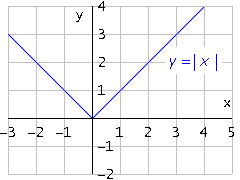
La función valor absoluto se define como:
Es de la forma f(x) = IxI, cuyo dominio son los reales y el rango son los reales mayores o iguales a cero. La grafica que se obtiene es una curva en forma de v.
EJEMPLO:
Ø
Ø FUNCIÒN RAIZ CUADRADA
Es una función que asigna a un argumento su raíz cuadrada positiva. Es de la forma f(x) = √x , donde el dominio de la función son los valores de x que hacen que el radicando sea positivo y el rango son los reales mayores o iguales a cero. La grafica que se obtiene es una curva ascendente que está por encima del eje x
Ejemplo:
Ø FUNCiÓN RACIONAL
Es una función de la forma f(x) = p(x)/q(x) , donde p(x) y q(x) son polinomios y q(x)≠0. La función racional no está definida para valores de x en el cual q(x) se hace diferente de cero, este valor al representarlo gráficamente es una asíntota. La grafica que se obtiene son curvas interrumpidas por la asíntota.
Ejemplo:
Ø FUNCIONES TRASCENDENTALES
FUNCIÓN EXPONENCIAL
FUNCIÓN EXPONENCIAL
Es una función de la forma f(x) = ax, donde a>o y a≠1 .cuyo dominio son los números reales y el rango son los reales mayores que cero. La grafica que se obtiene es una curva ascendente si a>1 y descendente si o<a<1.
Ejemplos:
Ø FUNCIÓN
Es una función inversa a la función exponencial, es de la forma
f(x) = logax, donde a>o y a≠1. La grafica que se obtiene es una curva simétrica a la función exponencial.
f(x) = logax, donde a>o y a≠1. La grafica que se obtiene es una curva simétrica a la función exponencial.
Ejemplos:
Ø FUNCIÓN
Las funciones trigonométricas surgen de estudiar el triangulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos lados cualesquiera dependen del valor de los ángulos del triangulo. Se distinguen seis tipos de funciones trigonométricas, Las cuales cada una de ellas tiene su dominio, rango, periodo y su gráfica es distinta, como son:
Ejemplos:
f(x) = sen x
f(x) = sen x
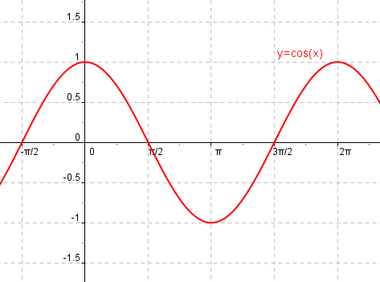
f(x) = cos x
f(x) = tan x
f(x) = cot x
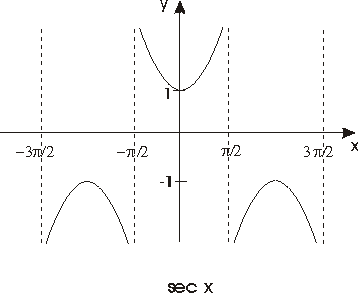
f(x) = sec x
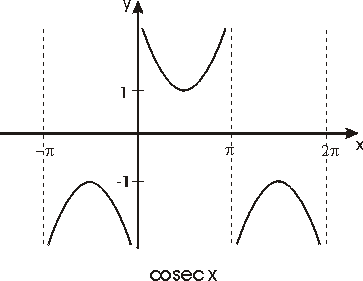
f(x) = cscx